Ellitticità

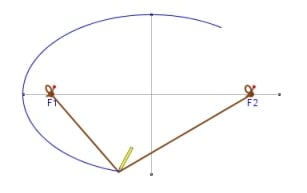
L'ellitticità (appiattimento o schiacciamento, indicato con la lettera f, iniziale del termine inglese flattening) di uno sferoide oblato definisce lo schiacciamento dei poli dello sferoide rispetto al suo equatore; una sfera ha un valore di ellitticità pari a 0, mentre un disco possiede un valore prossimo ad 1, ma mai uguale ad esso.

Un pianeta, o comunque qualunque altro corpo celeste di forma sferoidale, in rotazione tende ad assumere un aspetto schiacciato, a causa della forza centrifuga, responsabile anche del rigonfiamento equatoriale.

Definizione

Ci sono differenti varianti di ellitticità o appiattimento; nel caso sia necessario evitare confusione, la prima variante viene indicata come prima ellitticità.

Da un punto di vista strettamente matematico, la (prima) ellitticità è definita come:

${\displaystyle f={\frac {a-b}{a}}=1-\cos(o\!\varepsilon )=2\sin ^{2}\left({\frac {o\!\varepsilon }{2}}\right)={\mbox{versin}}(o\!\varepsilon ),}$

dove ${\displaystyle a}$ e ${\displaystyle b}$ sono rispettivamente i raggi equatoriale e polare del corpo, ${\displaystyle o\!\varepsilon }$ è l'eccentricità angolare (definita come ${\displaystyle o\!\varepsilon =\arcsin e}$, dove ${\displaystyle e}$ è l'eccentricità; oppure equivalentemente come ${\displaystyle o\!\varepsilon =\arccos {\frac {b}{a}}}$) e ${\displaystyle {\mbox{versin}}}$ è il senoverso.

Il grado di ellitticità dipende da diversi fattori, come:

• la relazione tra la forza di gravità e la forza centrifuga;
• le dimensioni e la densità del corpo;
• la sua rotazione e la sua elasticità.

Nel caso di un corpo fluido a densità uniforme, si ha un'approssimazione in funzione della costante di gravitazione universale, ${\displaystyle G}$, del periodo di rotazione ${\displaystyle T}$ e della densità ${\displaystyle \rho }$:

${\displaystyle f\approx {\frac {3\pi }{2GT^{2}\rho }}.}$

Esiste anche un'ellitticità di secondo grado, ${\displaystyle f'}$ (designata talvolta anche ${\displaystyle n}$), che è la tangente al quadrato della metà dell'eccentricità angolare:

${\displaystyle f'={\frac {a-b}{a b}}={\frac {1-\cos(o\!\varepsilon )}{1 \cos(o\!\varepsilon )}}=\tan ^{2}\left({\frac {o\!\varepsilon }{2}}\right).}$

Ellitticità dei corpi celesti

Tutti i corpi celesti presentano un certo grado di ellitticità. La Terra, ad esempio, possiede un'ellitticità nel WGS84 di 1:298,257223563, che corrisponde ad una differenza tra il raggio equatoriale e il raggio polare di circa 21,385 km (0,335%), impercettibile dallo spazio; il Sole possiede un'ellitticità di 1:1000, la Luna di circa 1:900. Al contrario, Giove e Saturno possiedono un'ellitticità elevata, rispettivamente di 1:16 ed 1:10, tanto che risulta visibile già con un piccolo telescopio amatoriale.

Note

Voci correlate

• Ellissoide di riferimento
• Rotazione
• Forza centrifuga
• Rigonfiamento equatoriale

Collegamenti esterni

• (EN) flattening, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Flattening, su MathWorld, Wolfram Research.